Este mes de Octubre participé en dos conferencias ágiles la Agile Tour Toulouse y la Agile Tour Vilnius y hablé de toma de decisiones con Bentoism.
¿Porque tomar decisiones es difícil?
Es difícil porque no estamos en un dominio de algo que se pueda medir cuantitativamente como mayor, menor o igual que otra opción, si no en un dominio normativo, en que lo que cuenta son nuestras preferencias, o interés propio. Desde Adam Smith, y con su punto culminante en el artículo publicado en 1970 “La responsabilidad social de los empresarios es incrementar sus ganancias” de Milton Friedman, el interés proprio suele estar reducido a uno mismo. Otras teorías como los Commons de Elinor Ostrom desafían esta visión del interés propio.
Además del interés propio en la toma de decisiones, el otro factor importante es el tiempo. El tiempo tiene una capacidad de transformar nuestros valores pero a la hora de decidir nos enfrentamos a la dificultad de imaginar el futuro, más fácil es recordar el pasado.
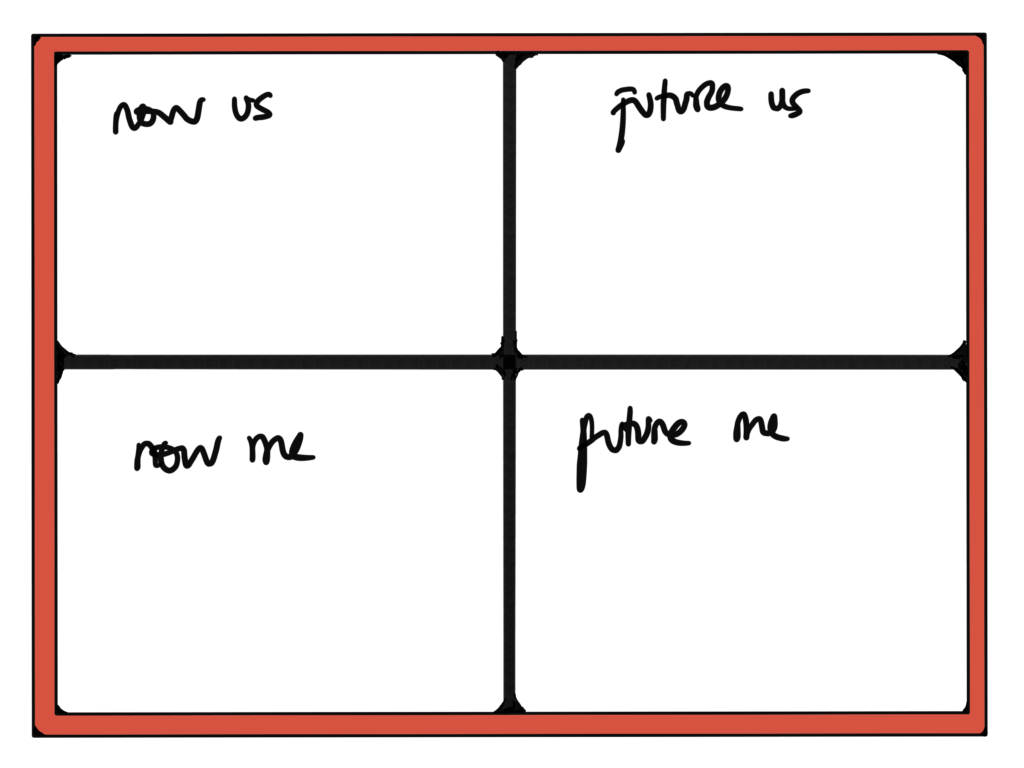
Entonces, ¿cómo podemos mirar la toma de decisiones más allá del corto plazo y de una visión reducida del interés proprio?
Escuché hablar del Bentoism con Yancey Strickler, autor de This could be our Future y cofundador de Kickstarter hace un año en el Web Summit. Desde ahí que viene formando una comunidad de practica internacional que intenta explorar los conceptos de yo y nosotros, ahora y en el futuro, basándose en la filosofía de las cajas de comida japonesas: Bento.